Sa, 27.12.2025 — Samuel Oppenheim
Ist das Weltall endlich oder unendlich groß? Dieses Problem hat der österreichische Astronom Samuel Oppenheim in einem populärwissenschaftlichen Vortrag im Verein zur Verbreitung naturwissenschaftlicher Kenntnisse in Wien diskutiert - zu einer Zeit als es die Big Bang Theorie noch nicht gab und die Leistungsfähigkeit der Fernrohre noch sehr beschränkt war. Oppenheim hat bedeutende Beiträge zur Himmelsmechanik, zur Sternkinematik, der Berechnung von Kometen- und Kleinplanetenbahnen und zum Einfluss der Gravitation geleistet.*
1860 wurde in Wien der (auch heute noch existierende) Verein zur Verbreitung naturwissenschaftlicher Kenntnisse gegründet. In dessen Rahmen wurden frei zugängliche, populäre Vorträge von Experten aus allen Fächern der Naturwissenschaften gehalten, deren Drucklegung und weite Verbreitung festgelegt war [1]. Zahlreiche berühmte Wissenschafter- beispielsweise Eduard Süess, Karl von Frisch, Stefan Meyer, Hermann Mark - haben hier Beiträge geliefert. Am 16. Dezember 1925 hat der bedeutende österreichische Astronom Samuel Oppenheim in diesem Verein über "Die Sterne und der Raum" berichtet [2].
|
Titelblatt des Vortrags (https://www.zobodat.at/pdf/SVVNWK_66_0019-0032.pdf) und Foto von Samuel Oppenheim (https://kuffner-sternwarte.at/sternwarte/vks_ksw_astronomen.php) |
Bau und Struktur des Raumes zu erforschen sowie die Frage nach seiner Endlichkeit und Unendlichkeit zu beantworten, ist eines der Hauptprobleme der modernen Astronomie, aber auch eines der schwierigsten. Es wäre am vollständigsten zu lösen durch eine Durchwanderung des ganzen Raumes, aber wir Menschen sind an die Erde gebunden und selbst mit unseren besten Flugzeugen können wir uns von ihr nur auf Strecken entfernen, die im Vergleiche zu den Dimensionen des ganzen Weltraumes als verschwindend zu betrachten sind. So sind wir nicht in der Lage, eine solche Wanderung auszuführen und auf ihr Beobachtungen zu sammeln, wie wir es auf der Erde ohne Schwierigkeit zu tun gewohnt sind und daher genötigt, nach einem anderen Wanderer Umschau zu halten, aus dessen hiebei gemachten Erfahrungen wir zu schöpfen und unsere Kenntnisse stetig zu vervollständigen haben.
Der Lichtstrahl
Ein solcher Wanderer ist der Lichtstrahl. Von den fernsten Himmelsräumen kommt er an unser Auge und erzählt uns in einer Sprache, die wir nur verstehen müssen, von den Sternen, die er auf seinem Wege getroffen. Er verkündet uns damit nicht bloß ihre Existenz, sondern auch die Richtung, in der sie zu sehen sind, auf deren Auffassung sich die Bestimmung ihres Ortes am Himmel gründet. Er erzählt uns ebenso, wenn wir ihn in einem Glasprisma analysieren, von der chemischen Beschaffenheit der Sterne und ihrer materiellen Zusammensetzung. Und was für uns heute die Hauptaufgabe ist, er erzählt uns auch einiges über die Länge des Weges, den er vom Sterne bis an unser Auge zurückgelegt hat, und damit über die Erstreckung der ganzen Sternenwelt, ob sie endlich oder unendlich ist, ob begrenzt oder unbegrenzt.
Das zur Beantwortung der letzten Frage notwendige Beobachtungsmaterial muß jedoch ein doppeltes sein. Es genügt nicht, einzig Distanzmessungen vorzunehmen, und aus ihnen die Ausdehnung des Sternraumes festzustellen, sondern es müssen noch rein statistische Abzählungen der Sterne hinzukommen, zur Festlegung des Gesetzes, nach dem deren Zahl mit der Größe zunimmt, um so über die Sternerfüllung des Raumes Auskunft zu geben.
Schätzung von Größe und Zahl der Sterne
Jeder Stern sendet uns nämlich eine bestimmte Menge Licht zu. Er hat eine. gewisse Leuchtkraft, wie man auch sagt eine bestimmte Größe. Sie ist für verschiedene Sterne verschieden und der Grund für diese Verschiedenheit entspringt zwei Ursachen. Der Stern kann an sich eine geringe Leuchtkraft haben, denn nichts sagt uns, daß alle Sterne gleiche; sogenannte absolute Leuchtkraft haben müssen, sowie wir auch auf der Erde Lichtquellen verschiedener Helligkeit besitzen, oder aber er kann recht hell sein und erscheint uns nur wegen seiner größeren Entfernung von der Erde schwächer als ein anderer, da die Helligkeit des Lichtes, wie bekannt, mit der Entfernung abnimmt. Darnach ist auch die Wirkung eines Fernrohrs, mit dessen Hilfe wir ja den Sternenhimmel durchforschen wollen, eine doppelte. Sie ist eine mehr raumdurchdringende, indem es uns schwächere Sterne zeigt, die nur wegen ihrer großen Entfernung von der Erde so erscheinen, und dann eine nachlesende, indem es uns auch tatsächlich lichtschwache Sterne zeigt.
|
Abbildung 2. Ein aktueller Blick ins ferne Universum: Die ersten Aufnahmen mit dem James Webb Teleskop (2022) zeigen die bislang tiefsten und schärfsten Infrarotbilder Tausender Galaxien im Sternhaufen SMACS 0723, wie sie vor 4,6 Milliarden Jahren erschienen. (Credit: NASA, ESA, CSA und STScI) |
Beobachten wir also den Sternenhimmel mit immer größeren Fernrohren, so wird die Zahl der Sterne stets zunehmen, aus dem einen wie aus dem anderen Grunde, und bei unbegrenztem und unendlichem Himmel auch ins Unendliche anwachsen. Ist aber die Sternenwelt endlich und begrenzt, so muß einmal die eine, und zwar die raumdurchdringende Kraft des Fernrohres ein Ende haben und nur die zweite Kraft wird noch vorhanden sein. Es muß sich an der Grenze der Sternenwelt eine Änderung des Gesetzes für die Zunahme der Sterne zeigen. Denn neue sehr helle Sterne, die nur wegen ihrer großen Entfernung von uns schwach erscheinen, sind nicht mehr da, sondern nur mehr an sich schwache, die uns eben unser großes lichtstarkes Fernrohr noch sichtbar macht.
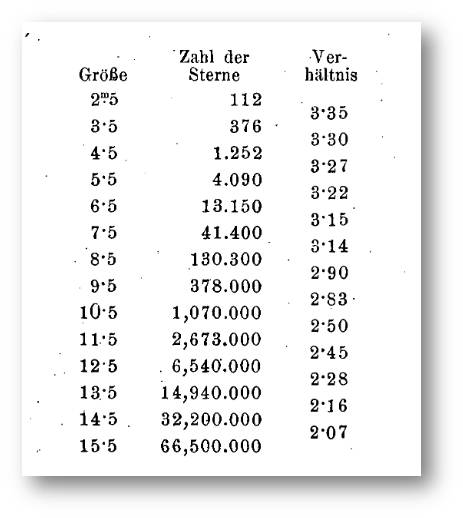
Die Beobachtungen lassen nun tatsächlich eine solche Änderung des Gesetzes in den Abzählungen der Sterne erkennen. Während, wie es die folgende Tabelle zeigt, die neben der Größe der Sterne (m) deren Gesamtzahl (stets von der Größe 0 angefangen) und ihre Zunahme (Verhältniszahl) angibt, diese Zunahme für die Sterne von der Größe 2,5 bis etwa 9,5 oder 10,5 noch als konstant, im Mittel zwischen 3,35 bis 2,83 angesehen werden kann, nimmt sie von da ab rasch ab (von 2,83 bis 2,07) und deutet damit an, daß etwa von der Größenklasse 10,5 ab die raumdurchdringende Kraft des Fernrohres erschöpft ist und, was nachher in ihm noch sichtbar wird, nur mehr Nachzügler sind, wirklich schwach leuchtende Sterne, die eben noch für unser Fernrohr erreichbar sind. (Anm. Redn.: Sternengrößen konnten vor 100 Jahren nur an Hand ihrer scheinbaren Größe -Helligkeit - (m) klassifiziert werden, wobei m = 1 die höchste Helligkeit, die folgenden Stufen jeweils 2,5 Mal geringere Helligkeit aufweisen.)
|
Scheinbare Größe (m) der Sterne, deren Zahl und die Relation von Größe und Zahl. |
Hiemit ist erwiesen, daß das sichtbare Sternsystem ein begrenztes ist, eine Insel im sonst vielleicht unendlichen Raum, und diese Begrenztheit ist nicht etwa der Ausdruck einer Beschränktheit in der Leistungsähigkeit des Fernrohres. Denn von Galilei an, der zum ersten Male ein Fernrohr gegen den Himmel richtete, bis auf Herschel, der mit seinem Riesenteleskop den Himmel durchmusterte und an verschiedenen Stellen Sternzählungen ausführte, hat die Zahl der Sterne mit wachsender Größe des Fernrohrs stets zugenommen. Erst neuestens, trotz Verwendung photographischer Daueraufnahmen, die oft Sterne bis zur 17—18ten Größe bringen, hat sich jedoch diese Vergrößerung nicht mehr in der gleichen Weise vollzogen. Sie wird immer geringer und strebt damit einer endlichen Grenze zu. Wie groß diese ist, läßt sich heute noch nicht mit einiger Sicherheit angeben. Im übrigen hat es wenig auf sich, ob sie an die 80, 90 oder gar 100 Millionen heranreicht. Das Wesentliche bleibt die Endlichkeit des ganzen Systems, was die Zahl der in ihm sichtbaren Einzelkörper anlangt.
Doch neben den Sternen zeigt uns der Himmel noch andere Körper, vorerst die Nebel in den verschiedensten teils regelmäßigen, teils ganz bizarren Formen, teils solche spiraliger Struktur, sowie endlich die Sternhaufen. Gehören auch sie, entsteht da die neue Frage, dem Sternsystem an, das wir als unser weiteres Vaterland zu betrachten haben — unser engeres ist das spezielle Sonnensystem — oder sind sie im Gegenteile von ihm ganz unabhängige Gebilde?
Distanz zur Erde
Diese Frage kann nur durch Ermittlung ihrer Distanz von der Erde entschieden werden. Hiezu stehen den Astronomen bekanntlich mehrere Wege offen. Sie beruhen teils auf Winkelmessungen (trigonometrische Parallaxen), teils und gerade in neuerer Zeit auf Untersuchungen der Spektra der Sterne (spektroskopische Parallaxen), teils werden sie auch aus der Größe der Eigenbewegungen abgeleitet. Speziell für die Sterne ergaben sich die in der folgenden Tabelle enthaltenen Mittelwerte der Parallaxen ihrer einzelnen Größenklassen und damit ihrer Entfernung von der Erde, ausgedrückt in Lichtjahren, als dem Weg, den das mit einer Geschwindigkeit von 300.000 km in der Sekunde sich bewegende Licht in einem Jahre zurücklegt und der etwa 10 Billionen km beträgt.
|
Zahlen, die einen Überblick über die räumliche Ausdehnung des Milchstraßensystems geben. |
Die gleichen Methoden, angewandt auf Nebel und Sternhaufen, gaben nun folgende Einzelwerte:
für den berühmten Orionnebel: π= 0"0054 = 600 Lichtjahre,
für den Sternhaufen der Plejaden: π = 0'-032 = 100 Lichtjahre,
für den Sternhaufen des Krebses: π= 0 , 0 2 4 = 135 Lichtjahre.
Aus ihnen ist zu schließen, daß diese wie viele andere unserem Sternsystem, angehören. Dagegen errechnete man:
für den schönen Kugelliaufen im Sternbild des Sobieskischen Schildes: π = 0"-0008 = 4000 Lichtjahre,
für den Kugelhaufen im Sternbild des Zentaurus: π = 0" 00015 = 21.000 Lichtjahre,
und als Mittelwert aus 69 solchen Kugelhaufen: π = 0" 000044 = 74.000 Lichtjahre.
Noch größere Distanzwerte erhielt man für die Spiralnebel, so für den schönen Spiralnebel im Sternbild der Andromeda π = 0,0000054 == 600.000 Lichtjahre, und, fügt man hinzu, daß dieser Nebel uns am Himmel in einer Größe von mehr als einem Grad erscheint, so folgt für seine lineare Ausdehnung ein Wert von 23.000 Lichtjahren oder einer Parallaxe von π=0,00014 von einem Ende bis zum andern, eine Ausdehnung, die weit die unseres Sternsystems übertrifft. Noch größere Werte für die Distanzen erhielt man für andere Spiralnebel.
Es unterliegt damit keinem Zweifel, daß diese, besonders die Spiralnebel neue Sternsysteme sind, unabhängig von unserem speziellen, und von ihm durch nach 10.000 von Lichtjahren zählende Distanzen getrennt. Ist auch deren Zahl endlich, sowie die Anzahl der Sterne in unserem System eine endliche ist, oder ist sie unendlich? Auf diese Frage gibt die Beobachtung bis nun keine Antwort. Sie sagt wohl, daß die Zahl der am Himmel sichtbaren Spiralnebel eine sehr große, aber immerhin nur eine endliche ist. Indes ob dies einer Unzulänglichkeit in der optischen Tragweite unserer Fernrohre zuzuschreiben ist oder einer tatsächlichen Beschränktheit ihrer Zahl, ist zur Zeit nicht zu entscheiden.
|
Abbildung 3. Aktueller Blick auf die Spiralgalaxie NGC 5584, die 72 Millionen Lichtjahre von der Erde entfernt ist. Unter den leuchtenden Sternen von NGC 5584 befinden sich pulsierende Sterne, sogenannte Cepheiden-Variable, und Supernovae vom Typ Ia, eine besondere Klasse explodierender Sterne, die. als zuverlässige Entfernungsmarker dienen, um die Expansion des Universums zu messen. (Credit: NASA, ESA, CSA, and A. Riess (STScI).) |
Ist aber das letztere der Fall, dann haben wir den Raum als von endlicher Große aufzufassen und die Vorstellung eines unendlichen Raumes ist zu verwerfen. Doch tritt hiebei die neue Frage nach seiner Begrenzung auf. Der unendliche Raum ist natürlich unbegrenzt, aber der endliche müßte an irgendeiner Stelle eine Grenze oder Schranke aufweisen. Wo ist diese und wie mag sie sich allenfalls in den Beobachtungen äußern?
Endlicher - unendlicher - gekrümmter Raum?
Es ist nun von Interesse zu hören, daß die Annahme einer endlichen Welt nicht notwendig auf die Existenz von Grenzen für ihn führt, sondern daß es auch einen endlichen und trotzdem unbegrenzten Raum geben, kann. Denke man sich eine Gerade, die ja nach zwei entgegengesetzten Richtungen ins Unendliche geht, ein ganz klein wenig aber stets in einem Sinne gekrümmt, denke man sich ferner eine Ebene, die ebenfalls ins Unendliche verläuft, in gleicher Art ein wenig und stets in einem Sinne gekrümmt, so heißt dies ein Wanderer längs der Geraden gehend, ebenso ein Wanderer auf der Ebene in irgendeiner Richtung vorwärts schreitend, wird wieder zu seinem Ausgangspunkte zurückkehren, ohne eine Grenze oder Schranke gefunden zu haben. Die Gerade schließt sich nämlich zu einem Kreise, die Ebene zu einer Kugel. Ein Beispiel hiefür ist das Reisen auf der Erdoberfläche. Jeder Horizont in jedem Punkte der Erde erscheint uns eben, und von der verschiedenen Lage dieser Horizonte an den aufeinanderfolgenden Stellen unserer Wanderung merken wir nichts, wenn wir unser Auge nur gegen die Erde gesenkt halten, sondern erst dann, wenn wir es nach dem Himmel richten und die Veränderungen beobachten, die hiebei viele Erscheinungen des Sternenhimmels zeigen.
Ähnlich kann es auch beim Raum sein. Durch die Annahme einer ganz geringen Krümmung für ihn kann erzielt werden, daß er sich schließt, wie die Gerade zu einem Kreise, die Ebene zu einer Kugel, und daß ein Wanderer, der jetzt die Erde verläßt und im Raume sich fortbewegt, wieder zu seinem Ausgangspunkt zurückkehrt oder, da ein solcher Wanderer nur das Licht sein kann, daß alle Lichtstrahlen geschlossene Linien sind. Ein solcher Raum würde uns das Bild einer Endlichkeit und doch Unbegrenztheit geben.
Wenn nicht wieder eine neue Schwierigkeit hinzukäme. Sie liegt in der merkwürdigen Eigenschaft eines solchen Raumes, daß sich in ihm; zwei Gerade nicht wie in einem ebenen Räume in einem, sondern in zwei Punkten schneiden. Daß dies der Fall ist, wird uns aus der Analogie mit der Kugel klar. Gehen auf einer solchen zwei Wanderer von einem Punkte aus, so entfernen sie sich anfangs voneinander bis zu einer gewissen maximalen Distanz, nähern sich sodann wieder, treffen sich in einem Punkte auf der entgegengesetzten Seite der Kugel, dem sogenannten Gegenpunkte, entfernen sich wieder voneinander bis zu einem gewissen Maximum, um dann erst in ihrem Ausgangspunkt zusammenzukommen. Ebenso ist es im gekrümmten Raum. Zwei Lichtstrahlen, die von einem leuchtenden Punkte ausgehen, treffen sich außer im Ausgangspunkte, auch noch im entgegengesetzt gelegenen, und da jeder leuchtende Punkt durch die von ihm ausgehenden Lichtstrahlen sichtbar wird, so entspricht ihm noch ein zweiter, der Gegenpunkt, in dem sich die Strahlen abermals vereinigen. Jeder Beobachter muß also jede Lichtquelle doppelt sehen, einmal in der Richtung des kürzeren Lichtweges, das Original, dann in der entgegengesetzten des längeren, sein Gegenbild. Alle Sterne müßten doppelt auftreten, als wirkliche und als Gegenbilder. Aber welcher uns sichtbare Stern der reelle, welcher nur sein Gegenbild ist, wäre uns natürlich unbekannt. Ebenso auch die Sonne und ihr Gegenbild, die Gegensonne, und fragen wir, wie hell diese Gegenbilder, also auch die Gegensonne sein müßte, so wäre die Antwort darauf: ebenso hell wie das Original. Denn eine kleine Fläche, wie die Pupille unseres Auges, die dem Lichtstrahle sich entgegenstellt, wird offenbar von einem Bündel von Lichtstrahlen, das von der realen Lichtquelle kommt, ebenso stark beleuchtet wie von einem, das vom Gegenbilde stammt. Bild und Gegenbild würden also in gleicher Helligkeit erstrahlen. Kurz wir hätten neben einer Sonne des Tages auch eine Sonne der Nacht.
Doch diese Überlegungen bedürfen einer Verbesserung. Sie sind nur dann vollauf richtig, wenn die Sonne und die Sterne im Raume ruhen. Wie die Beobachtungen erkennen lassen, ist dies, nicht der Fall. Vielmehr bewegen sie sich mit verschiedenen Geschwindigkeiten nach den verschiedensten Richtungen, die Sonne z. B. mit 20 km in der Sekunde nach dem Sternbild des Herkules. Dies hat zur Folge, daß, da die von der Sonne oder den Sternen ausgehenden Lichtstrahlen an dieser Bewegung nicht teilnehmen, die entsprechenden Gegenbilder sich im Räume verschieben, namentlich aber ihre Helligkeit sehr bedeutend geschwächt wird und sie vielleicht ganz unsichtbar sein können. Hiezu kommt außerdem noch die Möglichkeit einer Absorption des Lichtes durch den Sternen vorgelagerte Nebelmassen, die ebenfalls eine Schwächung besonders in der Helligkeit der Gegenbilder der Sterne bei dem langen und um den gekrümmten Raum zurückzulegenden Kreislauf des Strahles hervorrufen kann.
Damit erscheint die neue Auffassung über den Raum wieder gerettet; wohl macht sie dem Verständnis viele Schwierigkeiten und die Analogie mit der Kugel gibt nur einen schwachen Ersatz dafür ab, von ihm ein anschauliches Bild zu erlangen. Aber sie bietet doch viele Vorteile gegenüber der gebräuchlichen Vorstellung des unendlichen euklidschen Raumes, daß die Menschen sich bald werden bequemen müssen, sie als die richtigere, d. h. den physikalischen Erscheinungen entsprechendere anzusehen.
*Der vorliegende Artikel ist die ungekürzte Fassung des Manuskripts des Vortrags, den Samuel Oppenheimer am 15.12.1925 im Verein zur Verbreitung naturwissenschaftlicher Kenntnisse in Wien gehalten hat. Die ursprüngliche Schreibweise wurde beibehalten, es wurden aber von der Redaktion mehrere Untertitel und 2 aktuelle, vom James-Webb Teleskop ezeugte Blicke auf Ausschnitte des Universums eigefügt.
[1] Redaktion, 26.12.2014: Popularisierung der Naturwissenschaften im 19. Jahrhundert
[2] Verein zur Verbreitung naturwissenschaftlicher Kenntnisse: https://www.zobodat.at/pdf/SVVNWK_66_0019-0032.pdf (download unter www.biologiezentrum.at)
- Printer-friendly version
- Log in to post comments